はじめに
壁量計算③(四分割法)にて壁配置バランスのチェックが『不適』になった場合は、偏心率でバランスチェックする方法があります。
偏心率の方が詳細検討なので、四分割法で不適なプランでも適になることがあります。計算は少し難しいですが、設計の自由度がUPするので是非挑戦してみましょう。
それでは、偏心率について計算していきます。
↓この本も参考にしています。
偏心率とは
偏心率とは、重心と剛心のへだたりのねじり抵抗に対する割合として定義され、その数値が大きい程偏心の度合が大きくなります。言い換えると、耐力壁等の水平抵抗要素の平面的な偏りの大きいことを表しています。
建物の重さの中心を『重心』と呼びます。建物の耐力壁の配置による堅さの中心を『剛心』と呼びます。重心と剛心のずれを『偏心』と呼びます。つまり、重心と剛心が離れていると偏心が大きく、建物はねじれるようにして壊れます。
2000年(平成12年)の建築基準法改正で規定され、木造住宅においては『偏心率は0.3以下であること』を確認します。
壁配置バランス計算(偏心率)
偏心率は、各階のX方向とY方向にそれぞれ考え、①重心②剛心③偏心距離④ねじり剛性⑤弾力半径⑥偏心率の順で求めていきます。
順番に計算していけば、決して難しくありません。
それでは、計算していきましょう。
座標はどのようにとってもよいのですが、ここでは平面の左下隅(X0、Y0)から1m離れた点を原点として計算を進めていきます。
①重心
木造軸組工法において各階の重心は、各階共、固定荷重、積載荷重等が平面的に一様に分布していて、偏りがないものとして、平面の図心が重心に一致すると仮定します。
今回は、屋根部分の単位面積あたりの重量と、2階部分の単位面積あたりの重量の違いを考慮するための重み付け係数【引用:木造住宅の耐震診断と補強方法(2012年改訂版) P96】を用いて重心を求めていきます。
ここで、計算式はGx=Σ(W・X)/ΣWx、Gy=Σ(W・Y)/ΣWy
W:分割された長方形の個々の面積x重み付け係数(下表)
∑Wx,y:分割された長方形の個々の面積x重み付け係数(下表)の総計
X:分割された長方形の重心X座標
Y:分割された長方形の重心Y座標
| 床面積当たりの重量 (KN/㎡) | ||||
| 仕様 | 階数 | 1層目 | 2層目 | 3層目 |
| 軽い建物(石綿スレート板) | 平屋 | 1.43 | - | - |
| 2階建 | 2.15 | 1.43 | - | |
| 3階建 | 2.15 | 2.15 | 1.43 | |
| 重い建物(桟瓦葺) | 平屋 | 2.00 | - | - |
| 2階建 | 2.60 | 2.00 | - | |
| 3階建 | 2.60 | 2.60 | 2.00 | |
| 非常に重い建物(土葺瓦屋根) | 平屋 | 3.23 | - | - |
| 2階建 | 2.85 | 3.23 | - | |
| 3階建 | 2.85 | 2.85 | 3.23 |
※下階から『層』を数える。各糧物の最上層は、屋根の重量を示す。
まずは2階の重心を求めます。
下図は長方形に分割した時の中心と原点からの距離(X方向、Y方向)を表しています。
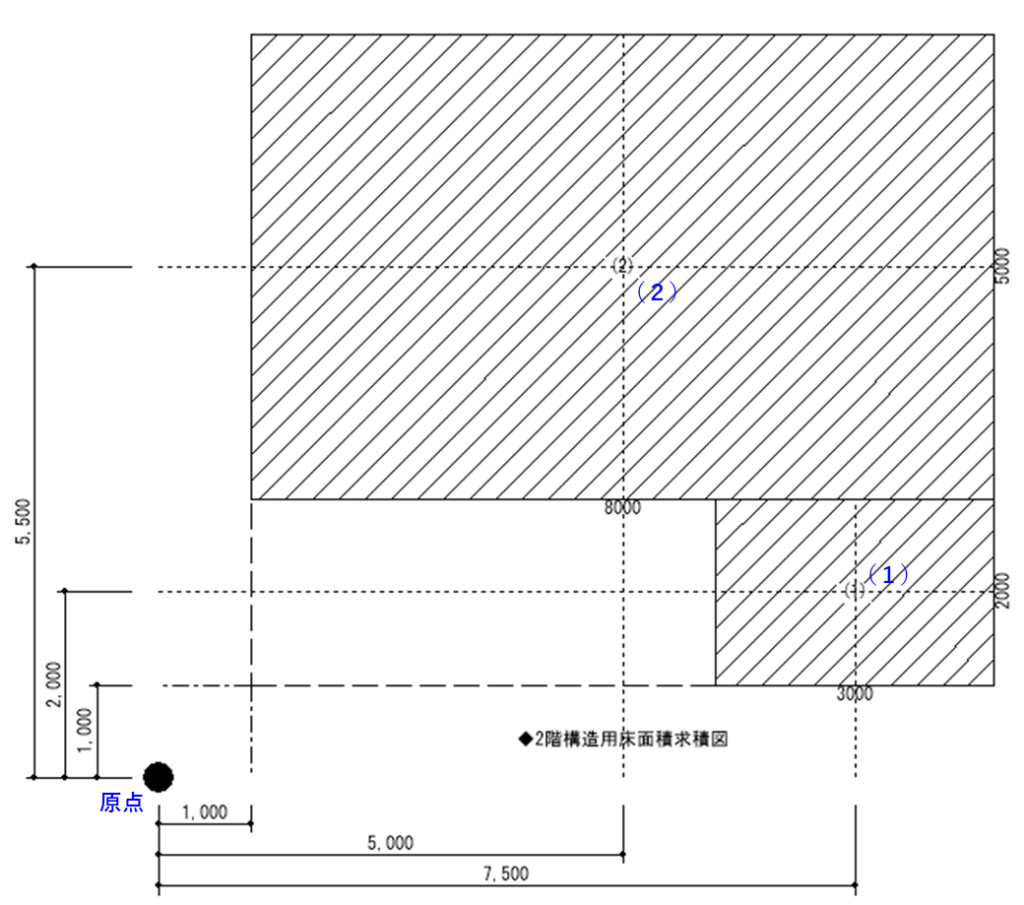
上図から
(1)は、面積(3x2=6㎡)と原点からの距離Xi(7.5m)、Yi(2m)となり、
(2)は、面積(8x5=40㎡)と原点からの距離Xi(5m)、Yi(5.5m)となります。
重み付け係数は、『軽い建物・2階建て・2層目』の1.43を用います。
以上の数値から、下表にまとめて2階の重心位置(X方向、Y方向)を計算します。
| 床面積(㎡) | 重付係数 | 区画重量 | 重心(m) | 区画重量×重心 | 重心G | |||||
| 階 | 番号 | Ai | K | Wi=Ai*K | Xi | Yi | ΣWx=Wi*Xi | ΣWy=Wi*Yi | Gx=ΣWx/Wi | Gy=ΣWy/Wi |
| 2 | (1) | 6.000 | ×1.43 | 8.5800 | 7.5 | 2.0 | 64.3500 | 17.1600 | ||
| (2) | 40.000 | ×1.43 | 57.2000 | 5.0 | 5.5 | 286.0000 | 314.6000 | |||
| 計 | 65.7800 | 350.3500 | 331.7600 | 5.3260 | 5.0434 | |||||
2階 重心計算表
次に1階の重心を求めます。
下図は長方形に分割した時の中心と原点からの距離(X方向、Y方向)を表しています。
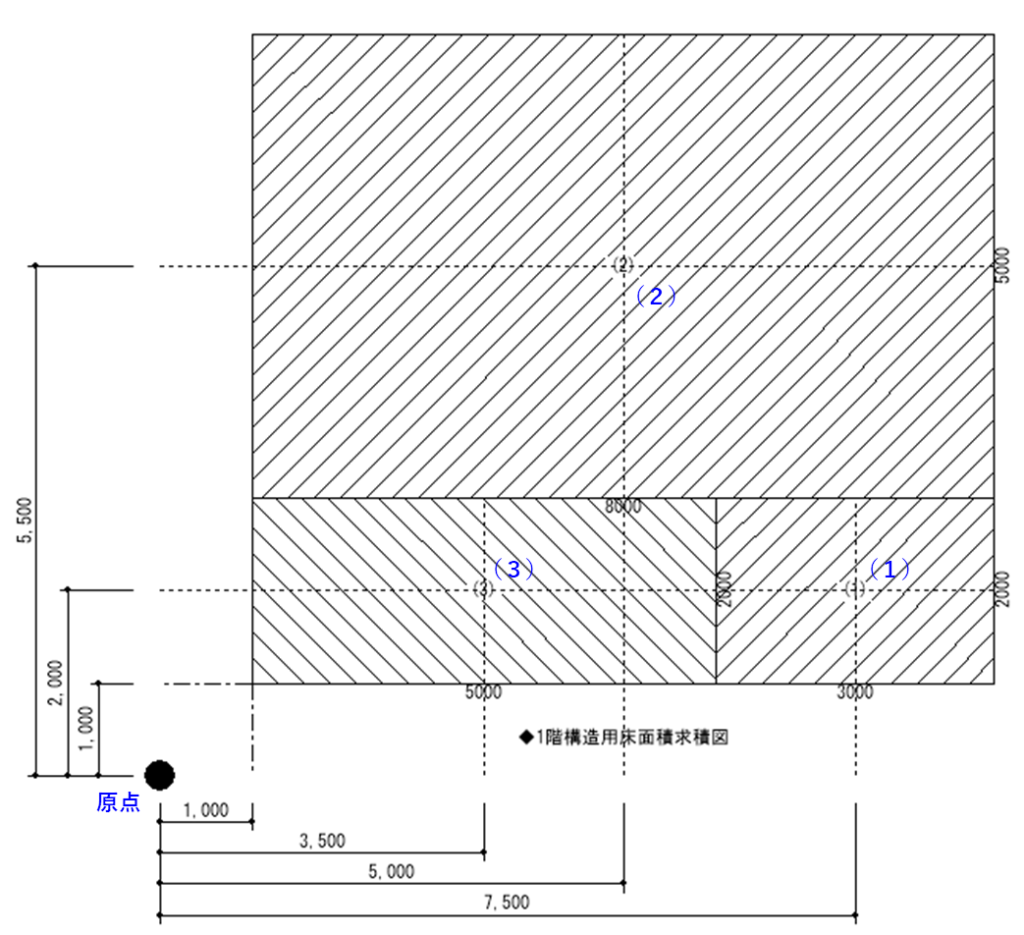
上図から
(1)は、面積(3x2=6㎡)と原点からの距離Xi(7.5m)、Yi(2m)となり、
(2)は、面積(8x5=40㎡)と原点からの距離Xi(5m)、Yi(5.5m)となり、
(3)は、面積(5x2=10㎡)と原点からの距離Xi(3.5m)、Yi(2m)となります。
重み付け係数は、(1)(2)は『軽い建物・2階建て・1層目』の2.15を用います。(3)はバルコニー部分になるので、『軽い建物・平屋・1層目』の1.43を用います。
以上の数値から、下表にまとめて1階の重心位置(X方向、Y方向)を計算します。
| 床面積(㎡) | 重付係数 | 区画重量 | 重心(m) | 区画重量×重心 | 重心G | |||||
| 階 | 番号 | Ai | K | Wi=Ai*K | Xi | Yi | ΣWx=Wi*Xi | Σwy=Wi*Yi | Gx=ΣWx/Wi | Gy=Σwy/Wi |
| 1 | (1) | 6.000 | x2.15 | 12.9000 | 7.5 | 2.0 | 96.7500 | 25.8000 | ||
| (2) | 40.000 | x2.15 | 86.0000 | 5.0 | 5.5 | 430.0000 | 473.0000 | |||
| (3) | 10.000 | x1.43 | 14.3000 | 3.5 | 2.0 | 50.0500 | 28.6000 | |||
| 計 | 113.200 | 576.8000 | 527.4000 | |||||||
| 合計(1階+2階) | 178.980 | 927.1500 | 859.1600 | 5.1801 | 4.8003 | |||||
1階 重心計算表
以上、重心が求まりました。
②剛心
耐力壁等の耐震要素の各計算方向(X方向及びY方向)の水平剛性をLx,Ly、その座標をX,Y、剛心の座標をSx,Syとし、各階の剛心を求めます。
ここで、計算式はSx=Σ(Ly・X)/ΣLy、Sy=Σ(Lx・Y)/ΣLx
Lx :X方向の有効耐力壁長さ = 壁倍率×壁実長
Ly :Y方向の有効耐力壁長さ = 壁倍率×壁実長
X:Y方向の耐力壁の中心X座標
Y:X方向の耐力壁の中心Y座標
まずは、2階の剛心を求めます。
下図は2階平面図の外周部に耐力壁を配置した『X方向の2階耐力壁』になります。長さ1mの耐力壁が13カ所あります。壁倍率は2.5倍です。
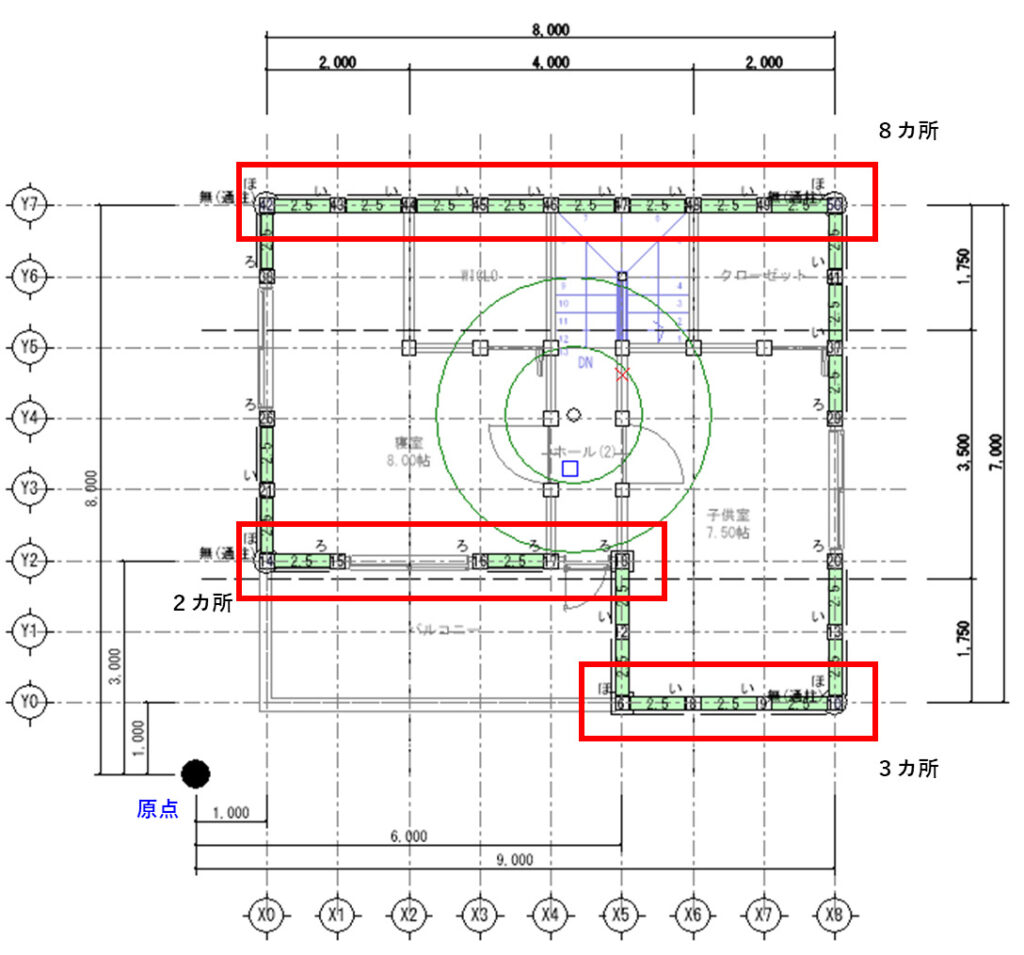
Y0通りは、壁倍率2.5の耐力壁が3カ所、Yi(1m)となり、
Y2通りは、壁倍率2.5の耐力壁が2カ所、Yi(3m)となり、
Y7通りは、壁倍率2.5の耐力壁が8カ所、Yi(8m)となります。
以上の数値から、下表にまとめて2階の剛心Syを計算します。
| 方向 | 階 | 存在壁量(m) | 距離(m) | 存在壁量x距離 | 剛心 | |||
| 壁倍率x | 長さx | 個数= | 計(Lxi) | Yi | Lxi*Yi | Sy=Σ(Lxi*Yi)/ΣLxi | ||
| X | 2 | 2.5 | 1 | 3 | 7.5000 | 1 | 7.5000 | |
| 2.5 | 1 | 2 | 5.0000 | 3 | 15.0000 | |||
| 2.5 | 1 | 8 | 20.0000 | 8 | 160.0000 | |||
| 計 | 32.5000 | 182.5000 | 5.6154 | |||||
2階 剛心計算表(Sy)
下図は2階平面図の外周部に耐力壁を配置した『Y方向の2階耐力壁』になります。長さ1mの耐力壁が10カ所あります。壁倍率は2.5倍です。
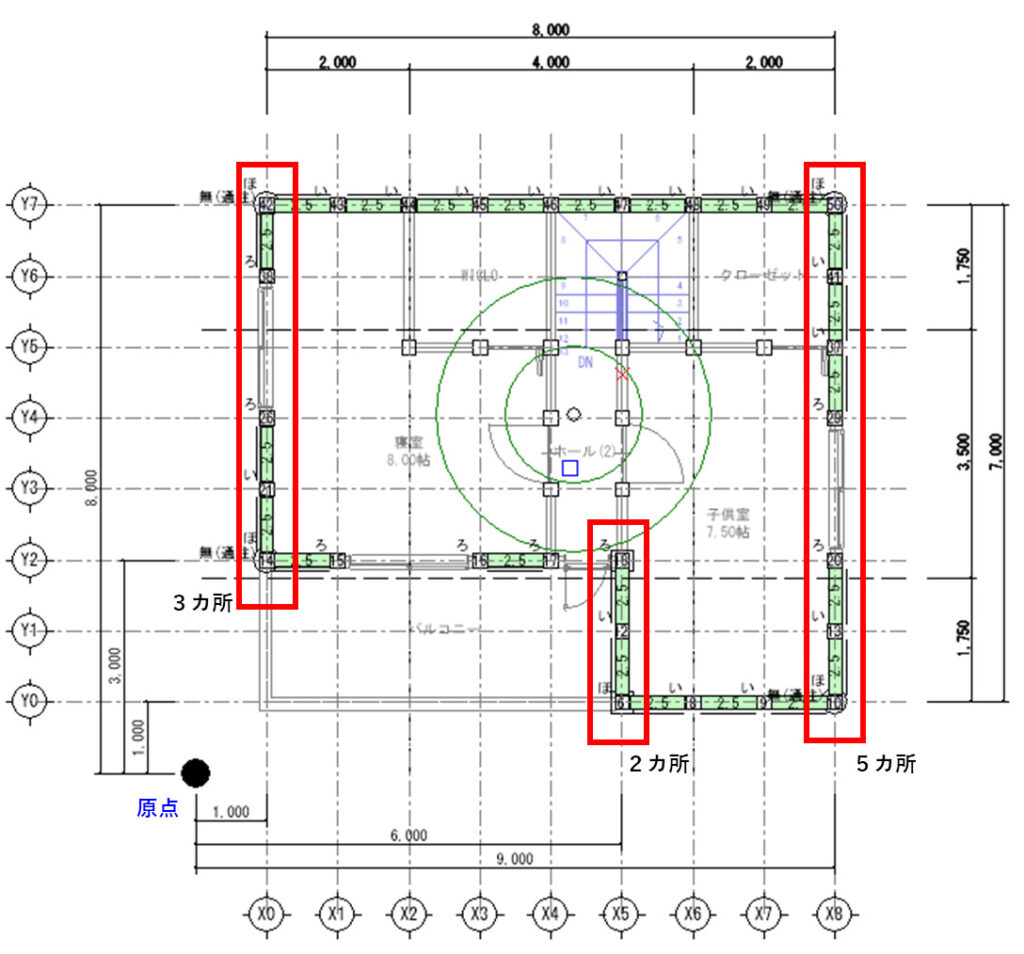
X0通りは、壁倍率2.5の耐力壁が3カ所、Xi(1m)となり、
X5通りは、壁倍率2.5の耐力壁が2カ所、Xi(6m)となり、
X8通りは、壁倍率2.5の耐力壁が5カ所、Xi(9m)となります。
以上の数値から、下表にまとめて2階の剛心Sxを計算します。
| 方向 | 階 | 存在壁量(m) | 距離(m) | 存在壁量x距離 | 剛心 | |||
| 壁倍率x | 長さx | 個数= | 計(Lyi) | Xi | Lyi*Xi | Sx=Σ(Lyi*Xi)/ΣLyi | ||
| Y | 2 | 2.5 | 1 | 3 | 7.5000 | 1 | 7.5000 | |
| 2.5 | 1 | 2 | 5.0000 | 6 | 30.0000 | |||
| 2.5 | 1 | 5 | 12.5000 | 9 | 112.5000 | |||
| 計 | 25.0000 | 150.0000 | 6.0000 | |||||
2階 剛心計算表(Sx)
下図は1階平面図の外周部に耐力壁を配置した『X方向の1階耐力壁』になります。長さ1mの耐力壁が9カ所あります。壁倍率は2.5倍です。
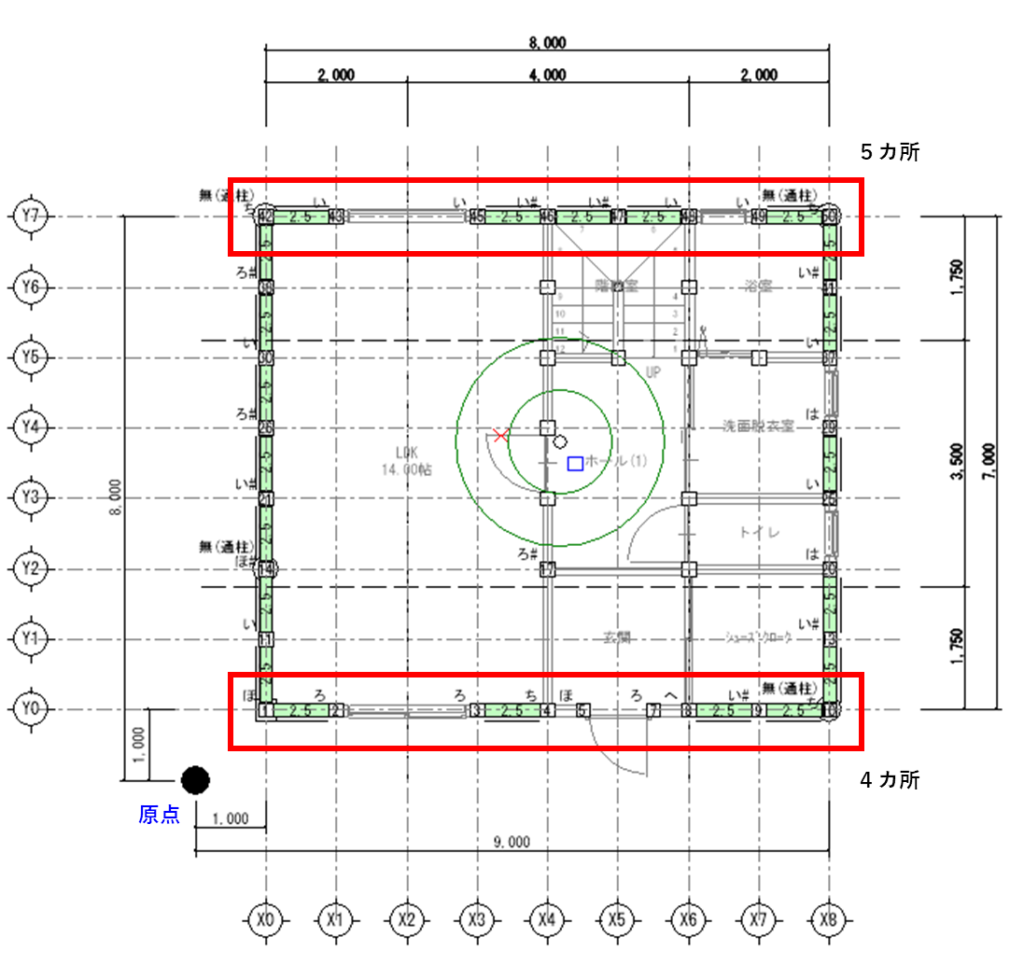
Y0通りは、壁倍率2.5の耐力壁が4カ所、Yi(1m)となり、
Y7通りは、壁倍率2.5の耐力壁が5カ所、Yi(8m)となります。
以上の数値から、下表にまとめて1階の剛心Syを計算します。
| 方向 | 階 | 存在壁量(m) | 距離(m) | 存在壁量x距離 | 剛心 | |||
| 壁倍率x | 長さx | 個数= | 計(Lxi) | Yi | Lxi*Yi | Sy=Σ(Lxi*Yi)/ΣLxi | ||
| X | 1 | 2.5 | 1 | 4 | 10.0000 | 1 | 10.0000 | |
| 2.5 | 1 | 5 | 12.5000 | 8 | 100.0000 | |||
| 計 | 22.5000 | 110.0000 | 4.8889 | |||||
1階 剛心計算表(Sy)
下図は2階平面図の外周部に耐力壁を配置した『Y方向の2階耐力壁』になります。長さ1mの耐力壁が12カ所あります。壁倍率は2.5倍です。
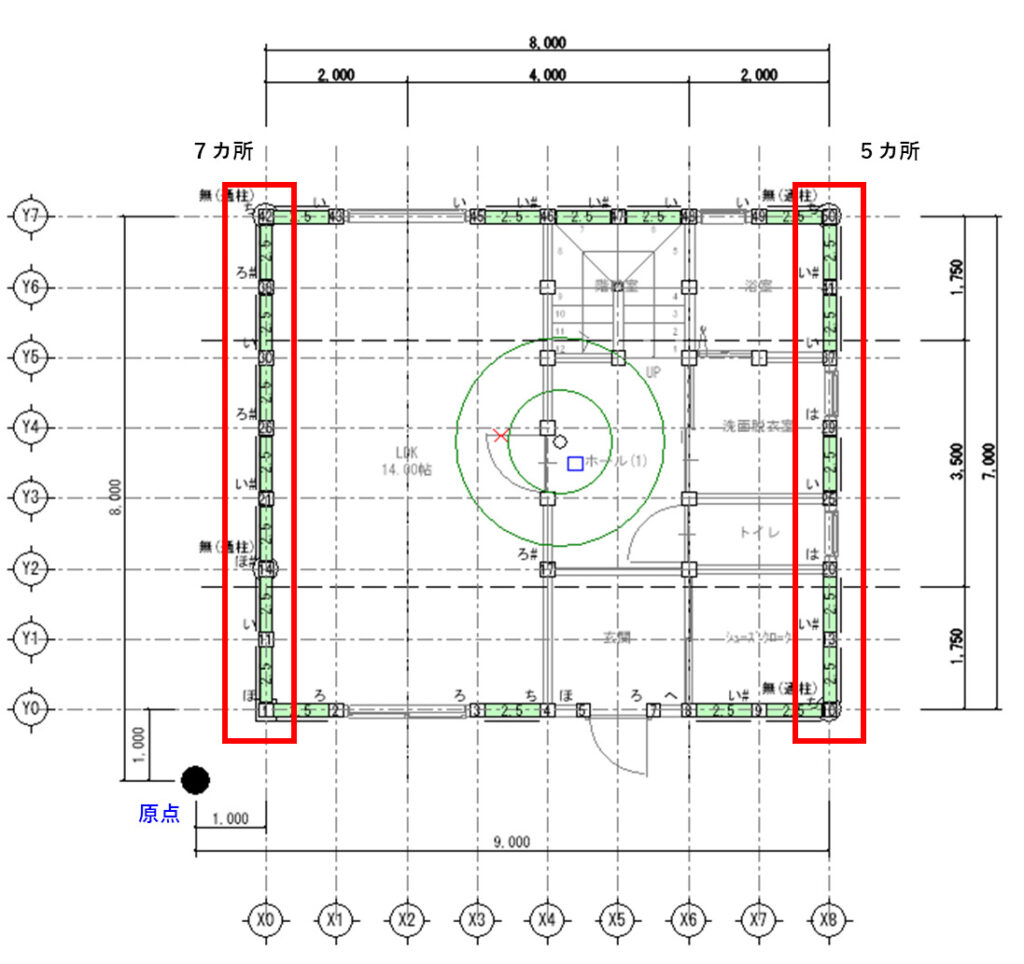
X0通りは、壁倍率2.5の耐力壁が7カ所、Xi(1m)となり、
X8通りは、壁倍率2.5の耐力壁が5カ所、Xi(9m)となります。
以上の数値から、下表にまとめて1階の剛心Sxを計算します。
| 方向 | 階 | 存在壁量(m) | 距離(m) | 存在壁量x距離 | 剛心 | |||
| 壁倍率x | 長さx | 個数= | 計(Lyi) | Xi | Lyi*Xi | Sx=Σ(Lyi*Xi)/ΣLyi | ||
| Y | 1 | 2.5 | 1 | 7 | 17.5000 | 1 | 17.5000 | |
| 2.5 | 1 | 5 | 12.5000 | 9 | 112.5000 | |||
| 計 | 30.0000 | 130.0000 | 4.3333 | |||||
1階 剛心計算表(Sx)
③偏心距離
偏心距離は、重心と剛心のズレになります。
計算は、重心と剛心の差の絶対値になります。
上記で求めた重心と剛心を下表にまとめて偏心距離を計算します。
| 階数 | 方向 | 重心G | 剛心S | 偏心距離e |
| ① | ② | |①-②| | ||
| 2 | X | 5.3260 | 6.0000 | 0.6740 |
| Y | 5.0434 | 5.6154 | 0.5720 | |
| 1 | X | 5.1801 | 4.3333 | 0.8468 |
| Y | 4.8003 | 4.8889 | 0.0886 |
偏心距離計算表
④ねじり剛性
ねじり剛性とは、ねじりに対する固さ表し、各階に剛心(Sx,Sy)周りのねじり剛性が発生します。
これは、各階ごとに1つ求めます。
剛心周りのねじり剛性KRは、下記計算式で求めます。
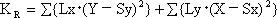
Lx :X方向の有効耐力壁長さ = 壁倍率×壁実長
Ly :Y方向の有効耐力壁長さ = 壁倍率×壁実長
X:Y方向の耐力壁の中心X座標
Y:X方向の耐力壁の中心Y座標
Sx:Y方向の耐力壁の剛心
Sy:Y方向の耐力壁の剛心
上記で求めた数値と計算式より、下表にまとめて2階のねじり剛性を計算します。
ねじり剛性の合計数値(607.6923)が答えになります。
| 方向 | 階 | 存在壁量(m) | 距離(m) | 剛心 | ねじり剛性 | |||
| 壁倍率x | 長さx | 個数= | 計(Lxi) | Yi | Sy | KR=Lxi*(Yi-Sy)^2 | ||
| ① | ② | ③ | ①*(②-③)の2乗 | |||||
| X | 2 | 2.5 | 1 | 3 | 7.5000 | 1 | 5.6154 | 159.7633 |
| 2.5 | 1 | 2 | 5.0000 | 3 | 34.2012 | |||
| 2.5 | 1 | 8 | 20.0000 | 8 | 113.7278 | |||
| 方向 | 階 | 存在壁量(m) | 距離(m) | 剛心 | ねじり剛性 | |||
| 壁倍率x | 長さx | 個数= | 計(Lyi) | Xi | Sx | KR=Lyi*(Xi-Sx)^2 | ||
| ① | ② | ③ | ①*(②-③)の2乗 | |||||
| Y | 2 | 2.5 | 1 | 3 | 7.5000 | 1 | 6.0000 | 187.5000 |
| 2.5 | 1 | 2 | 5.0000 | 6 | 0.0000 | |||
| 2.5 | 1 | 5 | 12.5000 | 9 | 112.5000 | |||
| 合計 | 607.6923 | |||||||
2階 ねじり剛性計算表
次に上記で求めた数値と計算式より、下表にまとめて1階のねじり剛性を計算します。
ねじり剛性の合計数値(738.8889)が答えになります。
| 方向 | 階 | 存在壁量(m) | 距離(m) | 剛心 | ねじり剛性 | |||
| 壁倍率x | 長さx | 個数= | 計(Lxi) | Yi | Sy | KR=Lxi*(Yi-Sy)^2 | ||
| ① | ② | ③ | ①*(②-③)の2乗 | |||||
| X | 1 | 2.5 | 1 | 4 | 10.0000 | 1 | 4.8889 | 151.2346 |
| 2.5 | 1 | 5 | 12.5000 | 8 | 120.9877 | |||
| 方向 | 階 | 存在壁量(m) | 距離(m) | 剛心 | ねじり剛性 | |||
| 壁倍率x | 長さx | 個数= | 計(Lyi) | Xi | Sx | KR=Lyi*(Xi-Sx)^2 | ||
| ① | ② | ③ | ①*(②-③)の2乗 | |||||
| Y | 1 | 2.5 | 1 | 7 | 17.5000 | 1 | 4.3333 | 194.4444 |
| 2.5 | 1 | 5 | 12.5000 | 9 | 272.2222 | |||
| 合計 | 738.8889 | |||||||
1階 ねじり剛性計算表
⑤弾力半径
弾力半径は、建物のねじりに対する抵抗の度合いを距離で表したものでX方向、Y方向それぞれを求めます。
計算式は re=√(KR/ΣL) となります。
ΣLx :X方向の有効耐力壁長さの合計
ΣLy :Y方向の有効耐力壁長さの合計
KR:ねじり剛性
上記で求めた数値と計算式より、下表にまとめて弾力半径を計算します。
| 階数 | 方向 | 有効耐力壁長さ計 | ねじり剛性 | 弾力半径 |
| ΣL | KR | re=√(KR/ΣL) | ||
| ① | ② | √①/② | ||
| 2 | X | 32.5000 | 607.6923 | 4.3241 |
| Y | 25.0000 | 4.9302 | ||
| 1 | X | 22.5000 | 738.8889 | 5.7305 |
| Y | 30.0000 | 4.9628 |
弾力半径計算表
⑥偏心率
最後に偏心率は、偏心距離÷弾力半径で求めます。
計算式は、ey/rex , ex/rey となります。
ex、ey :偏心距離
rex、rey:弾力半径
上記で求めた数値と計算式より、下表にまとめて偏心率を計算します。
| 階数 | 方向 | 偏心距離 | 弾力半径 | 計算式 | 偏心率 | 判定 |
| e | re | Re | ||||
| ① | ② | ①ey/②rex , ①ex/②rey | <0.3 | |||
| 2 | X | 0.6740 | 4.3241 | 0.5720÷4.3241= | 0.1323 | OK |
| Y | 0.5720 | 4.9302 | 0.6740÷4.9302= | 0.1368 | OK | |
| 1 | X | 0.8468 | 5.7305 | 0.0886÷5.7305= | 0.0155 | OK |
| Y | 0.0886 | 4.9628 | 0.8468÷4.9628= | 0.1707 | OK |
偏心率計算表
木造住宅においては『偏心率は0.3以下であること』と規定されていますので、計算結果により偏心率も問題ないことが分かりました。
最後に
今回は壁配置バランスについて、偏心率を計算しました。
どうだったでしょうか。少し計算が複雑で難しかったかもしれません。
掛け算や割り算だけでなく、ルートや乗数まで出てきたので何度も見返して学んでいただければと思います。
偏心率は重心と剛心のズレで決まり、ズレが大きいと地震力などの水平力を受けた時に変形が大きくなり、剛心周りを回転するように揺れることになります。
下図は、求めた『重心』『剛心』を平面図に転記したものになります。偏心率0.30の円より剛心が外側にあると変形が大きくなり、バランスが悪く『NG』ということになります。
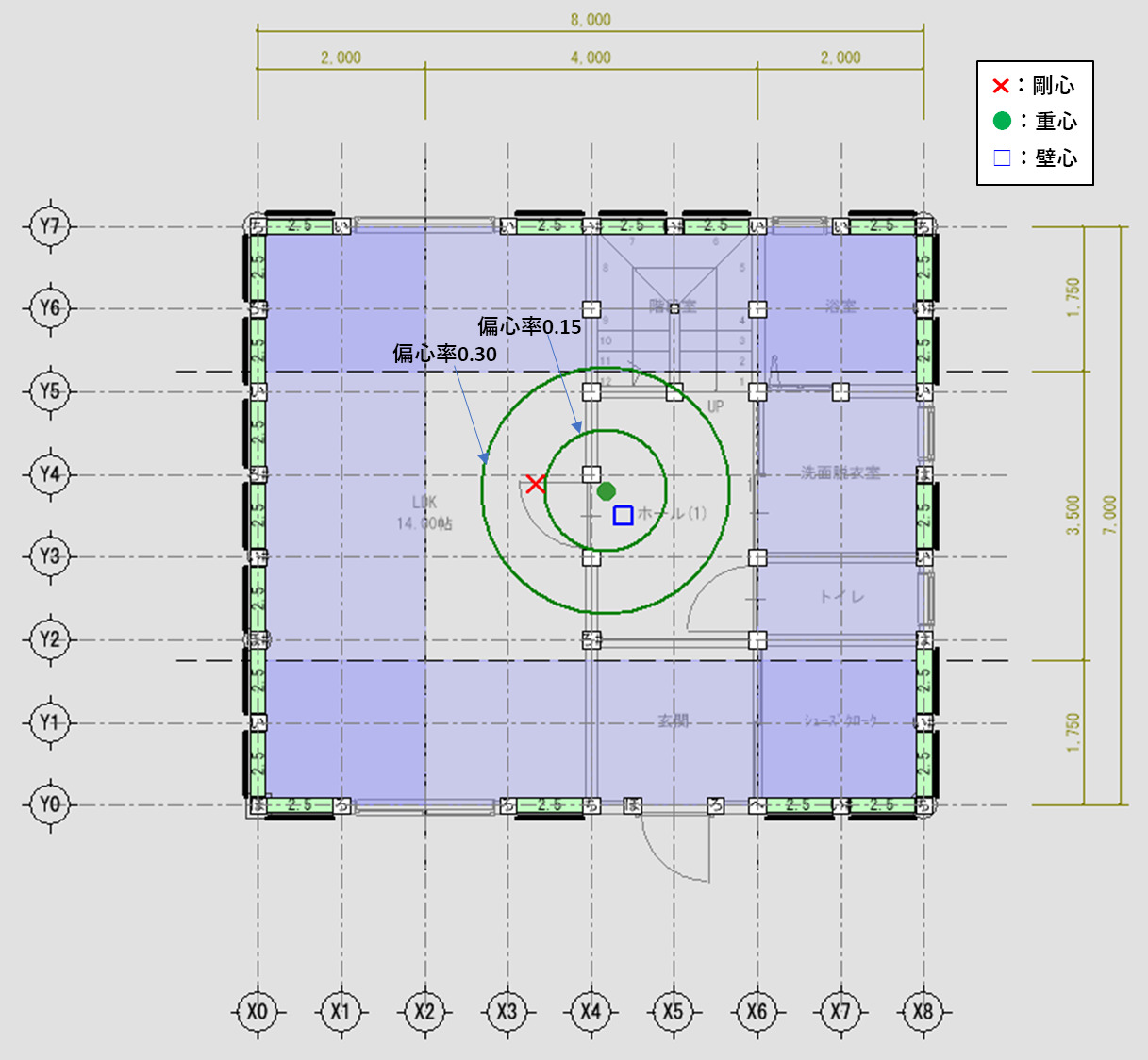
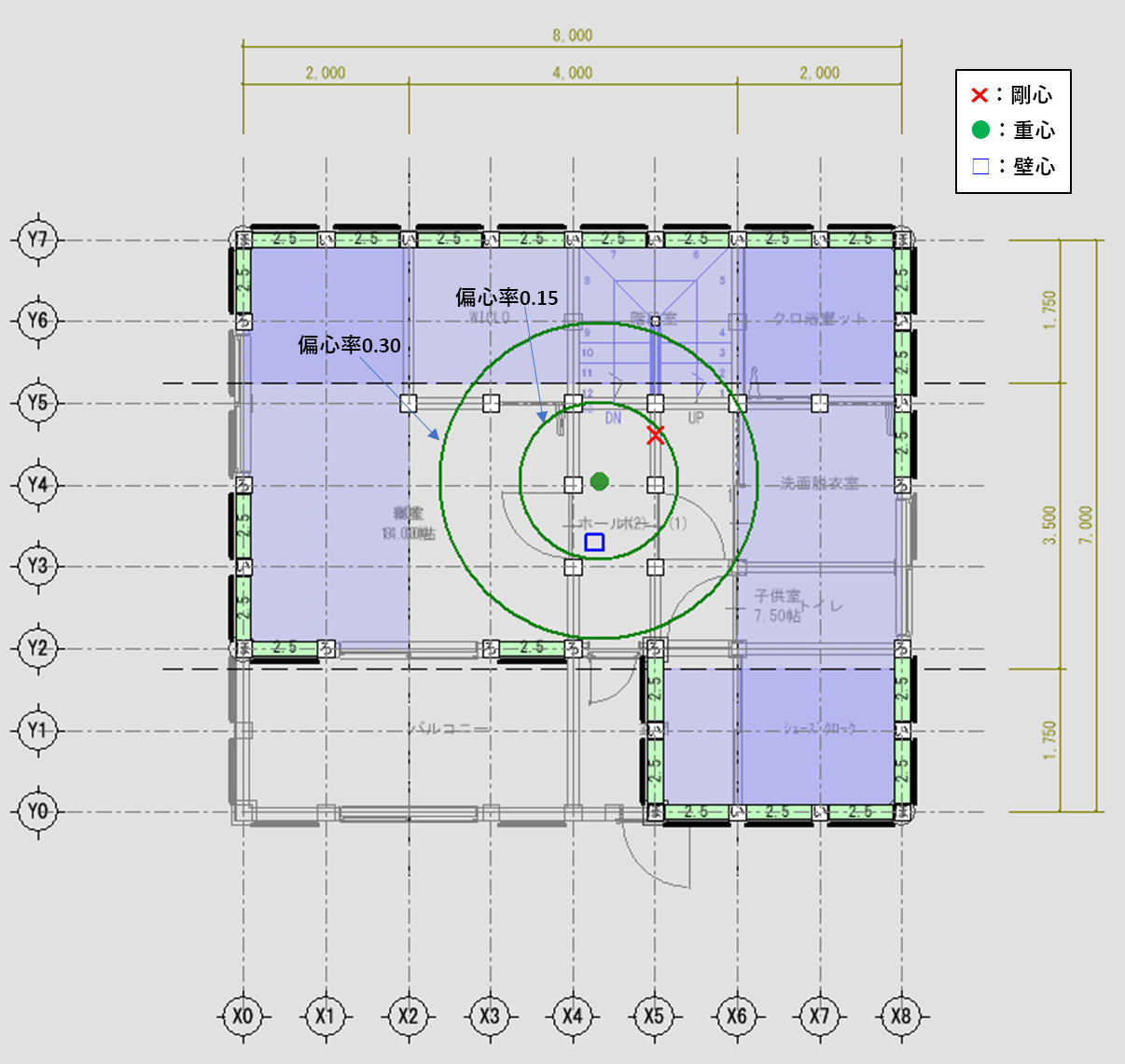
壁配置バランスについて問題ないことが確認できましたので、次回は、N値計算について計算します。